For rendering, I used to calculate normal matrix to transform vertex normal from model space to world space or view space. The normal matrix is defined as the inverse transpose of upper-left 3x3 matrix of the model matrix, from this article. Of course matrix inverse is not a cheap operation (I discussed more about matrix inverse here), and I just realized I actually don’t need to calculate inverse transpose at all, if the model matrix is made of translation, rotation and scale, which in most of the cases your matrices will be.

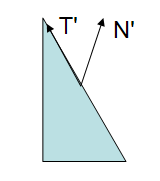
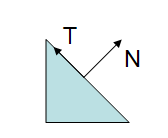
Let’s revisit the problem, why we cannot just use model matrix to transform the normal? If the matrix has uniform scale, there won’t be any problem. However if the matrix has non-uniform scale, after multiplied by the matrix, our normal is no longer perpendicular to the tangent anymore.

Now we describe the problem in math terms. Because we only transform direction, we can ignore the translation for convenience and use 3x3 matrix. The matrices used here are row major. Let our model matrix

be made of rotation (axis \(\vec{X}\), \(\vec{Y}\) and \(\vec{Z}\), where \(\vec{X}\cdot\vec{Y}=\vec{X}\cdot\vec{Z}=\vec{Y}\cdot\vec{Z}=0\), and \(\left|\vec{X}\right|=\left|\vec{Y}\right|=\left|\vec{Z}\right|=1\)), and scale \((a,b,c)\). We also have tangent \(\vec{T}=(T_0,T_1,T_2)\) and normal \(\vec{N}=(N_0,N_1,N_2)\), that \(\vec{T}\cdot\vec{N}=0\). Now after transform, tangent becomes \(\vec{T'}=\vec{T}M=a{T_0}\vec{X}+b{T_1}\vec{Y}+c{T_2}\vec{Z}\), we need to find a normal \(\vec{N'}\) such that \(\vec{T'}\cdot\vec{N'}=0\).

Remember \(\vec{X}\), \(\vec{Y}\) and \(\vec{Z}\) are unit axes perpendicular to each other, if we denote \(\vec{N'}={N'_0}\vec{X} + {N'_1}\vec{Y} + {N'_2}\vec{Z}\), we can expand this dot product.

Doesn’t this look familiar? We already know the original tangent and normal \(\vec{T}\cdot\vec{N}={T_0}{N_0} + {T_1}{N_1} + {T_2}{N_2}=0\). We can easily get our “transformed” normal

It means instead of calculating inverse transpose of model matrix, and send a 3x3 matrix to the shader, you can simply calculate reciprocal of squared scale and send over a vector3, use that to rescale your normal and multiply by the model matrix you already have, and that’s it. Because the calculation is cheap, you can even avoid sending over extra data, and just calculate the whole thing in vertex shader (3 dot product to get squared scale from model matrix, 3 reciprocal and multiply).

Of course the normal you get need to be re-normalized, but you need to do this no matter which method you use. Moreover since you have to re-normalize the normal in pixel shader anyway (because after interpolation the normal may not be of unit length), you don’t need to do anything extra in vertex shader.

Now how does the normal matrix handle the same problem? The inverse of our 3x3 model matrix is

It should be easy to confirm \(MM^{-1}=I\). More about matrix inverse can be found here.

The normal matrix is \(M'={(M^{-1})}^{T}=\left( \begin{matrix} \frac{1}{a}\vec{X} \\ \frac{1}{b}\vec{Y} \\ \frac{1}{c}\vec{Z} \\ \end{matrix} \right)\).

The transformed normal is \(\vec{N'}=\vec{N}M'=\frac{N_0}{a}\vec{X} + \frac{N_1}{b}\vec{Y} + \frac{N_2}{c}\vec{Z}\).

Well, we got the same result.

One thing to be careful about is, this method only works if the matrix axes are perpendicular to each other, that is \(\vec{X}\cdot\vec{Y}=\vec{X}\cdot\vec{Z}=\vec{Y}\cdot\vec{Z}=0\). If your matrix is made of translation, rotation and scale, this is always true. However if you have interesting coordinate system that this does not hold, you need to fall back to using normal matrix. The proof and explanation for normal matrix in a general case can be found in this original article.